EDIT: A complete revamp of PyTorch was released today (Jan 18, 2017), making this blogpost a bit obselete. I will update this post with a new Quickstart Guide soon, but for now you should check out their documentation.</a>
This Blogpost Will Cover:
- Part 1: PyTorch Installation
- Part 2: Matrices and Linear Algebra in PyTorch
- Part 3: Building a Feedforward Network (starting with a familiar one)
- Part 4: The State of PyTorch
Pre-Requisite Knowledge:
Torch is one of the most popular Deep Learning frameworks in the world, dominating much of the research community for the past few years (only recently being rivaled by major Google sponsored frameworks Tensorflow and Keras). Perhaps its only drawback to new users has been the fact that it requires one to know Lua, a language that used to be very uncommon in the Machine Learning community. Even today, this barrier to entry can seem a bit much for many new to the field, who are already in the midst of learning a tremendous amount, much less a completely new programming language.
However, thanks to the wonderful and billiant Hugh Perkins, Torch recently got a new face, PyTorch... and it's much more accessible to the python hacker turned Deep Learning Extraordinare than it's Luariffic cousin. I have a passion for tools that make Deep Learning accessible, and so I'd like to lay out a short "Unofficial Startup Guide" for those of you interested in taking it for a spin. Before we get started, however, a question:
Why Use a Framework like PyTorch? In the past, I have advocated learning Deep Learning using only a matrix library. For the purposes of actually knowing what goes on under the hood, I think that this is essential, and the lessons learned from building things from scratch are real gamechangers when it comes to the messiness of tackling real world problems with these tools. However, when building neural networks in the wild (Kaggle Competitions, Production Systems, and Research Experiments), it's best to use a framework.
Why? Frameworks such as PyTorch allow you (the researcher) to focus exclusively on your experiment and iterate very quickly. Want to swap out a layer? Most frameworks will let you do this with a single line code change. Want to run on a GPU? Many frameworks will take care of it (sometimes with 0 code changes). If you built the network by hand in a matrix library, you might be spending a few hours working out these kinds of modifications. So, for learning, use a linear algebra library (like Numpy). For applying, use a framework (like PyTorch). Let's get started!
For New Readers: I typically tweet out new blogposts when they're complete @iamtrask. Feel free to follow if you'd be interested in reading more in the future and thanks for all the upvotes on Hacker News and Reddit! They mean a lot to me.
Part 1: Installation
Install Torch: The first thing you need to do is install torch and the "nn" package using luarocks. As torch is a very robust framework, the installation instructions should work well for you. After that, you should be able to run:
luarocks install nn
and be good to go. If any of these steps fails to work, copy paste what looks like the "error" and error description (should just be one sentence or so) from the command line and put it into Google (as is common practice when installing).
Clone the Repository: At the time of writing, PyTorch doesn't seem to be in the PyPI repository. So, we'll need to clone the repo in order to install it. Assuming you have git already installed (hint hint... if not go install it and come back), you should open up your Terminal application and navigate to an empty folder. Personally, I have a folder called "Laboratory" in my home directory (i.e. "cd ~/Laboratory/"), which cators to various childhood memories of mine. If you're not sure where to put it, feel free to use your Desktop for now. Once there, execute the commands:
git clone https://github.com/hughperkins/pytorch.git
cd pytorch/
pip install -r requirements.txt
pip install -r test/requirements.txt
source ~/torch/install/bin/torch-activate
./build.sh
For me, this worked flawlessly, finishing with the statement
Finished processing dependencies for PyTorch===4.1.1-SNAPSHOT
If you also see this output at the bottom of your terminal, congraulations! You have successfully installed PyTorch!
Startup Jupyter Notebook: While certainly not a requirement, I highly recommend playing around with this new tool using Jupyter Notebok, which is definitely best installed using conda. Take my word for it. Install it using conda. All other ways are madness.
Part 2: Matrices and Linear Algebra
In the spirit of starting with the basics, neural networks run on linear algebra libraries. PyTorch is no exception. So, the simplest building block of PyTorch is its linear algebra library.
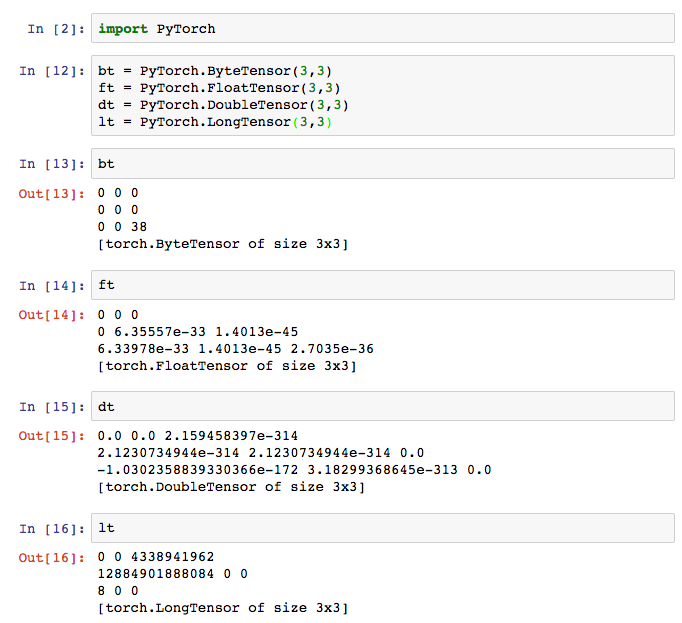
Above, I created 4 matrices. Notice that the library doesn't call them matrices though. It calls them tensors.
Quick Primer on Tensors: A Tensor is just a more generic term than matrix or vector. 1-dimensional tensors are vectors. 2-dimensional tensors are matrices. 3+ dimensional tensors are just refered to as tensors. If you're unfamiliar with these objects, here's a quick summary. A vector is "a list of numbers". A matrix is "a list of lists of numbers". A 3-d tensor is "a list of lists of lists of numbers". A 4-d tensor is... See the pattern? For more on how vectors and matrices are used to make neural networks, see my first blog post on a Neural Network in 11 lines of Python
PyTorch Tensors There appear to be 4 major types of tensors in PyTorch: Byte, Float, Double, and Long tensors. Each tensor type corresponds to the type of number (and more importantly the size/preision of the number) contained in each place of the matrix. So, if a 1-d Tensor is a "list of numbers", a 1-d Float Tensor is a list of floats. As a general rule of thumb, for weight matries we use FloatTensors. For data matrices, we'll likely use either FloatTensors (for real valued inputs) or Long Tensors (for integers). I'm a little bit surprised to not see IntTensor anywhere. Perhaps it has yet to be wrapped or is just non-obvious in the API.
The final thing to notice is that the matries seem to come with lots of rather random looking numbers inside (but not sensibly random like "evenly random between 0 and 1"). This is actually a plus of the library in my book. Let me explain (skip 1 paragraph if you're familiar with this concept)
Why Seemingly Nonsenical Values: When you create a new matrix in PyTorch, the framework goes and "sets aside" enough RAM memory to store your matrix. However, "setting aside" memory is completely different from "changing all the values in that memory to 0". "Setting aside" memory while also "changing all the values to 0" is more computationally expensive. It's nice that this library doesn't assume you want the values to be any particular way. Instead, it just sets aside memory and whatever 1s and 0s happen to be there from the last program that used that piece of RAM will show up in your matrix. In most cases, we're going to set the values in our matrices to be something else anyway (say... our input data values or a specific kind of random number range). So, the fact that it doesn't pre-set the matrix values saves you a bit of processing time, but the user needs to recognize that it's their responsibility to actively choose the values he/she wants in a matrix. Numpy is not like this, which make Numpy a bit more user friendly but also less computationally efficient.
Basic Linear Algebra Operations: So, now that we know how to store numbers in PyTorch, lets talk a bit about how PyTorch manipulates them. How does one go about doing linear algebra in PyTorch?
The Basic Neural Network Operations: Neural networks, amidst all their complexity, are actually mostly made up of rather simple operations. If you remember from A Neural Network in 11 Lines of Python, we can build a working network with only Matrix-Matrix Multiplication, Vector-Matrix Multiplication, Elementwise Operations (addition, subtraction, multiplication, and division), Matrix Transposition, and a handful of elementwise functions (sigmoid, and a special function to compute sigmoid's derivative at a point which uses only the aforementioned elementwise operations). Let's initialize some matrices and start with the elementwise operations.

Elementwise Operations: Above I have given several examples of elementwise addition. (simply replacing the "+" sign with - * or / will give you the others). These act mostly how you would expect them to act. A few hiccups here and there. Notably, if you accidentally add two Tensors that aren't aligned correctly (have different dimensions) the python kernel crashes as opposed to throwing an error. It could be just my machine, but error handling in wrappers is notoriously time consuming to finish. I expect this functionality will be worked out soon enough, and as we will see, there's a suitable substitute.
Vector/Matrix Multiplication: It appears that the native matrix multiplication functionality of Torch isn't wrapped. Instead, we get to use something a bit more familiar. (This feature is really, really cool.) Much of PyTorch can run on native numpy matrices. That's right! The convenient functionality of numpy is now integrated with one of the most popular Deep Learning Frameworks out there. So, how should you really do elementwise and matrix multipliplication? Just use numpy! For completeness sake, here's the same elementwise operations using PyTorch's numpy connector.

And now let's see how to do the basic matrix operations we need for a feedforward network.

Other Neural Functions: Finally, we also need to be able to compute some nonlinearities efficiently. There are both numpy and native wrappers made available which seem to run quite fast. Additionally, sigmoid has a native implementation (something that numpy does not implement), which is quite nice and a bit faster than computing it explicitly in numpy.

I consider the fantastic integration between numpy and PyTorch to be one of the great selling points of this framework. I personally love prototyping with the full control of a matrix library, and PyTorch really respects this preference as an option. This is so nice relative to most other frameworks out there. +1 for PyTorch.
Part 3: Building a Feedforward Network
In this section, we really get to start seeing PyTorch shine. While understanding how matrices are handled is an important pre-requisite to learning a framework, the various layers of abstraction are where frameworks really become useful. In this section, we're going to take the bare bones 3 layer neural network from a previous blogpost and convert it to a network using PyTorch's neural network abstractions. In this way, as we wrap each part of the network with a piece of framework functionality, you'll know exactly what PyTorch is doing under the hood. Your goal in this section should be to relate the PyTorch abstractions (objects, function calls, etc.) in the PyTorch network we will build with the matrix operations in the numpy neural network (pictured below)s.
import PyTorch
from PyTorch import np
def nonlin(x,deriv=False):
if(deriv==True):
return x*(1-x)
return 1/(1+np.exp(-x))
X = np.array([[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]])
y = np.array([[0],
[1],
[1],
[0]])
np.random.seed(1)
# randomly initialize our weights with mean 0
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in range(60000):
# Feed forward through layers 0, 1, and 2
l0 = X
l1 = nonlin(np.dot(l0,syn0))
l2 = nonlin(np.dot(l1,syn1))
# how much did we miss the target value?
l2_error = y - l2
if (j% 10000) == 0:
print("Error:" + str(np.mean(np.abs(l2_error))))
# in what direction is the target value?
# were we really sure? if so, don't change too much.
l2_delta = l2_error*nonlin(l2,deriv=True)
# how much did each l1 value contribute to the l2 error (according to the weights)?
l1_error = l2_delta.dot(syn1.T)
# in what direction is the target l1?
# were we really sure? if so, don't change too much.
l1_delta = l1_error * nonlin(l1,deriv=True)
# lets update our weights
syn1 += l1.T.dot(l2_delta)
syn0 += l0.T.dot(l1_delta)
Error:0.496410031903 Error:0.00858452565325 Error:0.00578945986251 Error:0.00462917677677 Error:0.00395876528027 Error:0.00351012256786
Now that we've seen how to build this network (more or less "by hand"), let's starting building the same network using PyTorch instead of numpy.
import PyTorch from PyTorchAug import nn from PyTorch import np
First, we want to import several packages from PyTorch. np is the numpy wrapper mentioned before. nn is the Neural Network package, which contains things like layer types, error measures, and network containers, as we'll see in a second.
# randomly initialize our weights with mean 0 net = nn.Sequential() net.add(nn.Linear(3, 4)) net.add(nn.Sigmoid()) net.add(nn.Linear(4, 1)) net.add(nn.Sigmoid()) net.float()
The next section highlights the primary advantage of deep learning frameworks in general. Instead of declaring a bunch of weight matrices (like with numpy), we create layers and "glue" them together using nn.Sequential(). Contained in these "layer" objects is logic about how the layers are constructed, how each layer forward propagates predictions, and how each layer backpropagates gradients. nn.Sequential() knows how to combine these layers together to allow them to learn together when presented with a dataset, which is what we'll do next.
X = np.array([[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]]).astype('float32')
y = np.array([[0],
[1],
[1],
[0]]).astype('float32')
This section is largely the same as before. We create our input (X) and output (y) datasets as numpy matrices. PyTorch seemed to want these matrices to be float32 values in order to do the implicit cast from numpy to PyTorch tensor objects well, so I added an .astype('float32') to ensure they were the right type.
crit = nn.MSECriterion() crit.float()
This one might look a little strange if you're not familiar with neural network error measures. As it turns out, you can measure "how much you missed" in a variety of different ways. How you measure error changes how a network prioritizes different errors when training (what kinds of errors should it take most seriously). In this case, we're going to use the "Mean Squared Error". For a more in-depth coverage of this, please see Chapter 4 of Grokking Deep Learning.
for j in range(2400):
net.zeroGradParameters()
# Feed forward through layers 0, 1, and 2
output = net.forward(X)
# how much did we miss the target value?
loss = crit.forward(output, y)
gradOutput = crit.backward(output, y)
# how much did each l1 value contribute to the l2 error (according to the weights)?
# in what direction is the target l1?
# were we really sure? if so, don't change too much.
gradInput = net.backward(X, gradOutput)
# lets update our weights
net.updateParameters(1)
if (j% 200) == 0:
print("Error:" + str(loss))
And now for the training of the network. I have annotated each section of the code with near identical annotations as the numpy network. In this way, if you look at them side by side, you should be able to see where each operation in the numpy network occurs in the PyTorch network.
One part might not look familiar. The "net.zeroGradParameters()" basically just zeros out all our "delta" matrices before a new iteration. In our numpy network, this was the l2_delta variable and l1_delta variable. PyTorch re-uses the same memory allocations each time you forward propgate / back propagate (to be efficient, similar to what was mentioned in the Matrices section), so in order to keep from accidentally re-using the gradients from the prevoius iteration, you need to re-set them to 0. This is also a standard practice for most popular deep learning frameworks.
Finally, Torch also separates your "loss" from your "gradient". In our (somewhat oversimplified) numpy network, we just computed an "error" measure. As it turns out, your pure "error" and "delta" are actually slightly different measures. (delta is the derivative of the error). Again, for deeper coverage, see Chatper 4 of GDL.
Putting it all together
import PyTorch
from PyTorchAug import nn
from PyTorch import np
# randomly initialize our weights with mean 0
net = nn.Sequential()
net.add(nn.Linear(3, 4))
net.add(nn.Sigmoid())
net.add(nn.Linear(4, 1))
net.add(nn.Sigmoid())
net.float()
X = np.array([[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]]).astype('float32')
y = np.array([[0],
[1],
[1],
[0]]).astype('float32')
crit = nn.MSECriterion()
crit.float()
for j in range(2400):
net.zeroGradParameters()
# Feed forward through layers 0, 1, and 2
output = net.forward(X)
# how much did we miss the target value?
loss = crit.forward(output, y)
gradOutput = crit.backward(output, y)
# how much did each l1 value contribute to the l2 error (according to the weights)?
# in what direction is the target l1?
# were we really sure? if so, don't change too much.
gradInput = net.backward(X, gradOutput)
# lets update our weights
net.updateParameters(1)
if (j% 200) == 0:
print("Error:" + str(loss))
Error:0.2521711587905884 Error:0.2500123083591461 Error:0.249952495098114 Error:0.24984735250473022 Error:0.2495250701904297 Error:0.2475520819425583 Error:0.22693687677383423 Error:0.13267411291599274 Error:0.04083901643753052 Error:0.016316475346684456 Error:0.008736669085919857 Error:0.005575092509388924
Your results may vary a bit. I do not yet see how random numbers are to be seeded. If I come across that in the future, I'll add an edit.
Part 4: The State of PyTorch
While still a new framework with lots of ground to cover to close the gap with its competitors, PyTorch already has a lot to offer. It looks like there's an LSTM test case in the works, and strong promise for building custom layers in .lua files that you can import into Python with some simple wrapper functions. If you want to build feedforward neural networks using the industry standard Torch backend without having to deal with Lua, PyTorch is what you're looking for. If you want to build custom layers or do some heavy sequence2sequence models, I think the framework will be there very soon (with documentation / test cases to describe best practices). Overall, I'm very excited to see where this framework goes, and I encourage you to Star/Follow it on Github
For New Readers: I typically tweet out new blogposts when they're complete at @iamtrask. Feel free to follow if you'd be interested in reading more in the future and thanks for all the upvotes on hacker news and reddit!